
<모집단과 표본집단>
1. 통계에서는 모집단을 연산 하지 않는다. 표본을 통해서 추정하는 학문이다.
2. 사실 우리는 모집단이 정규분포를 따르는 것과 상관없이 모집단을 대상으로 측정하고자 했던 값의 대표값(평균값)과
모집단의 개체들이 이 대표값으로부터 평균적으로 얼마나 떨어져있는지(표준편차)만으로 많은 정보를 얻을 수 있다.
3. 다행이 모집단의 평균값과 표준편차는 표본으로부터 구할 수 있음이 중심극한정리를 통해 수학적으로 증명되었다.
3. 따라서 모수 추정을 위해 통계학의 모든 관심은 표본집단이다. (*명확히는 표본의 통계분포)
<통계학의 연산 대상>
통계학에서 관심있는 대상은 대표값과 대표값이 갖는 오차이다.
1. 통계학에서 대표값은 평균이다. 평균값이 집단을 대표한다.
2. 그러나 모든 표본 통계값이 그렇듯이 표본 통계량은 추정값으로 오차를 포함하고 있다.
3. 따라서 표분분산은 이러한 오차의 정도를 가늠하기 위해 표준편차(or 분산)이 표본을 대표하는 통계값(평균)의 신뢰도를 평가할 수 있는 중요한 통계량이 되는 것이다.
4. 물론 중심극한 정리에 따라 모분산을 측정하는데도 사용.
5. 표본의 평균 = 모집단을 추정하기 위한 수단 , 표본의 분산 = 통계량의 신뢰도 + 모집단 분산 추정
모집단의 평균 = 집단의 대표값 , 모집단의 분산 = 모집단의 분포 추정
<중심극한정리>
1. 모집단의 분포에 상관없이 표본통계량(표본,분산)의 기대값은 모수로 추정된다. (같다고 하진 않겠다_포스팅7,8)
2. 표본을 추출하는 모집단이 서로 독립적이라면 여러 모집단에서 추출한 표본이더라도 표본평균의 분포는 정규분포이다.
3. 자연현상은 매우 복잡하다. 따라서 하나라고 생각했던 것이 둘로 이루어져 있을 경우도 많고, 대상 자체가 복잡할 수 있다. 이런 측면에서 중심극한정리는 실생활에 응용하기 위한 가장 중요한 전제이다.
<정규분포가 중요한 이유>
1. 우리는 중심극한 정리로 표본집단 통계량의 기대값을 통해 모수를 추정할 수 있는 정규분포를 얻을 수 있다.
2. 그러나 아무리 통계량을 불편추정량으로 맞추고 난 뒤 기대값으로 모수를 추정한다고 해도 어디까지나 추정이다.
3. 즉 미세하지만 오차를 갖는다.
4. 따라서 정규분포를 띄고 있음을 이용하여 그 오차의 신뢰도를 측정할 수 있다.
5. 대부분의 분석대상을이 정규분포를 띄고 있음에 정규분포를 가정으로 통계기법이 대다수 정리되었다.(ex. Z분포)
6. 물론 t-test도 그렇지만 정규분포일 때와 정규분포가 아닐 때로 계산 방법이 나눠져있지만 디폴트는 항상 정규분포다.
*불편추정량
불편추정량 개념을 이해하는 것이 쉽지 않다.
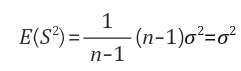
위 예시는 분산의 불편추정량이다.
모수와 동일하게 하기 위해 표본분산의 기대값은 n이 아닌 n-1로 계산할 수 밖에 없었다. 뭐 이런 느낌으로 받아들이자.
이 글이 포스팅되게끔 했던 블로그글 출처
1. 정규성 검정 : hsm-edu.tistory.com/243?category=828185,
2. 표본평균의 평균이 모평균과 같은 이유 : hsm-edu.tistory.com/14
3. 복원추출과 비복원추출에 대한 오해 : hsm-edu.tistory.com/980
4. 자유도와 불편추정량 : hsm-edu.tistory.com/13?category=741767
5. 비복원추출일 경우 표본평균의 평균과 분산 : hsm-edu.tistory.com/979?category=806920
6. 표본분산의 기댓값이 모분산과 같은 이유 : hsm-edu.tistory.com/979?category=806920
7. *중심극한 정리는 무엇이고 왜 중요한가? : drhongdatanote.tistory.com/57?category=648822
8. 불편추정량, 자유도 등 : www.youtube.com/playlist?list=PLmljWRabIwWBxh8V6eIODIz--B802mdLt
9. 중심극한정리 개념소개 : www.youtube.com/watch?v=iTNHQXGIEuU&lc=Ugzi_usvKfoni3_u8L14AaABAg.9JvfBZ9uc_w9JvfhsK94FB
'통계' 카테고리의 다른 글
| 확률 기본 개념 (0) | 2021.02.19 |
|---|---|
| 릿지 회귀 / 라쏘 회귀 / 일래스틱 회귀분석 (0) | 2021.01.25 |
| 확률밀도함수 그리고 KDE (0) | 2021.01.21 |
| T-value / F-value에 대한 본질적 통찰 (0) | 2021.01.17 |
| 평균,편차,공분산, 상관계수 (0) | 2021.01.04 |



