데이터가 skew 되어 있으면 항상 log변환한다라고 거의 암기하듯 받아들였다.
다른 다양한 포스팅들을 보며 도대체 로그변환을 왜 하는 것인지 한번 알아보자.
< 1. 로그스케일링 원리 >
출처 : bpapa.tistory.com/66
데이터 분석에서 log의 중요성에 대해서 이야기 해보겠다.
데이터 분석을 하기 위해 log를 취하는 이유는 한마디로 정규성을 높이고 분석(회귀분석 등)에서 정확한 값을 얻기 위함이다.
데이터 간 편차를 줄여 왜도1(skewness)와 첨도2(Kurtosis)를 줄일 수 있기 때문에 정규성이 높아진다.
예를 들어, 연령 같은 경우에는 숫자의 범위가 약 0세~120세 이하 이겠지만, 재산 보유액 같은 경우에는 0원에서 몇 조단위까지 올라갈 수 있다. 즉, 데이터 간 단위가 달라지면 결과값이 이상해 질 수 있다.
: log 변환은 1/ 큰 수를 작게 만들 경우 2/ 복잡한 계산을 간편하게 위할 경우 사용된다.
로그를 취하는 순간 그 수는 진수가 되어버리니, 값이 작아지고
로그의 성질에 따라 곱셈은 진수의 덧셈으로 나누기는 뺄셈으로 바뀐다.
[큰수를 작게 만들 경우]
예를 들어, 100= 이다. 100에 상용로그를 취한다면 100을 10을 밑으로 하는 지수가 있는 값의 그 지수로 나타낸다.
그래서 100에 상용로그를 취하면 2가 된다.
[복잡한 계산을 간편하게 만들 경우]
또한 로그를 취하면 로그의 성질에 의해 곱하기가 더하기로, 나누기가 빼기로 바뀐다.
결론적으로 식에 로그릴 취하는 이유는 큰 수를 작게 만들고, 복잡한 계산을 쉽게 만들고, 왜도와 첨도를 줄여서 데이터 분석 시 의미있는 결과를 도출하기 위한 것이다.
위의 재산 보유액 예와 같이 분석하려는 데이터 간의 편차가 큰 경우에 로그를 취하면 의미있는 결과를 얻을 가능성이 높아진다.
아래 차트에도 나와 있듯이 로그를 취하면 큰 값은 작아지는 것을 볼 수 있다.
위 포스팅으로 느낌을 잡았다면
'로그스케일링 원리'를 피부로 느껴보자.
로그 값을 취할 경우 큰 수에 대한 간격이 좁아지기 때문에
데이터 간 간격이 클 경우 유용하게 작용할 수 있다.
> 밑을 10으로 하는 로그는 10제곱 수 단위로 작동한다. (cf.상용로그가 아닌 자연로그를 취하는 경우도 봄)
따라서 10~100 구간의 '제곱 단위 차이'는 '정수'로,
동일 제곱 수 단위 안에서의 값 차이는 소숫점자리로 나타나게 된다.
ex. log13 = 1.11394335231
log113 = 2.05307844348

위 이미지 링크 영상을 보면 더 자세히 로그변환에 대해 느낌을 잡을 수 있을 것이다.

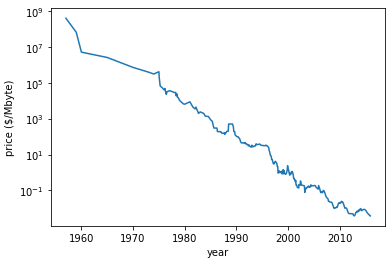
로그변환은 꼭 정규분포 변환에 한정되지 않음을 보여준 좋은 예시.
1960년대의 큰 차이를 보는 값들은 log로 인해 그 차이의 스케일이 작아지고 (ex 제곱단위의 정수 변화)
1970~2010의 값도 log변환으로 스케일이 작아졌지만 60년 값에 비해 그 폭이 작다. (ex 제곱 안 수의 소수자리 변화)
따라서 전체 스케일이 평준화되도록 각 값들이 작아졌기 때문에 분석이 용이해졌다.
출처: https://evening-ds.tistory.com/31 [저녁에 하는 데이터 공부]
< 2. 로그변환에 대한 고찰 >
회귀분석을 하다보면, 또는 회귀분석을 한 논문을 보다보면 변수에 로그를 취하는 경우가 종종 있다. 사실 꽤 많이 있다. 보통 노동경제학 논문에서 임금이나 소득을 쓰는 경우엔 여지없이 로그임금 또는 로그소득을 쓰고, GDP나 인구를 변수로 쓰는 경우도 로그GDP나 로그인구를 사용하는 경우가 꽤 많다. 계량경제학 서적을 보다보면 로그를 취한 변수를 해석하는 방법이 따로 있을 정도로 로그변환이 분명 중요하긴 하다. 하지만 그 중요성에 비해서 로그변환에 대해 자세히 설명하는 게 조금 부족하기는 하다. 예를 들어 '로그를 써야 하는 경우가 있는걸까?', '변수에 로그변환을 해야 하는 규칙 같은 게 있는 걸까?', '어떤 경우에 로그를 쓰고, 어떤 경우에는 변환을 하지 않을까?'와 같은 질문에 답을 바로 내리기가 어렵다.
결론적으로, 그런 법칙은 없는 것 같다. 아마 그래서 따로 설명이 안되어 있는 것은 아닌가 싶기도 하다. 다만 로그를 쓰는 게 더 나은 경우들은 있다. 비록 의무적으로 변환을 해야 하는 건 아니더라도. 다만, 이 내용은 경험적으로 또는 지도를 받으며 은연중에 알게 된 사실들이다보니 공인된 지식이라고 보기는 어렵다. 하지만 어느 정도 알아두면 교수님들의 공격(...)을 방어할 수단 중 하나는 될 수 있지 않을까 싶다. 그러기를 바라기도 하고.
아무튼 내 생각엔 대략 3가지 정도의 이유로 로그변환을 하는 것 같다.
1) 단위(Scale)의 문제
소득이 불평등에 미치는 영향에 관심이 있다고 해보자. 그러면 우리는 다음과 같은 생각을 하고 있다는 의미이다.

는 다른 설명변수 벡터를 말한다. 소득이 불평등에 미치는 효과를 추정하기 위해 선형식을 세운다고 해보자. 그리고 관심의 대상을 구체적으로 지역단위로 좁혀보자.
그러면 이제 관심사가 지역별 소득이 지역별 불평등에 미치는 영향으로 좁혀지고서 다음과 같은 선형식을 생각할 수 있다.
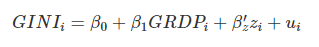
는 가 아닌 변수들의 벡터, 는 다른 변수들의 계수를 모아둔 벡터를 말한다. 지역별 소득은 GRDP로, 지역별 불평등은 지니계수로 통제한다고 가정했다. 자, 이제 이 식을 추정한 결과 우리의 관심대상인 이 X로 추정되었다고 해보자(예를 들어 0.0001이나 0.8213 이런 숫자).
그러면 우린 이걸 이렇게 해석한다. "다른 조건이 일정할 때 GRDP가 한 단위 늘어나면 지니계수는 평균적으로 X만큼 상승한다/하락한다."라고.
여기서 잠깐. GRDP가 한 단위 상승한다는 건 무슨 의미인가. 만약 우리가 GRDP를 천원, 백만원 같은 단위가 아니라 '원'으로 측정했으면 GRDP가 1원이 늘어나면 지니계수가 XX만큼 변한다는 의미이다. 이 값이 0.0001이라면, GRDP를 10,000원만 늘어나면 지니계수는 1이 증가한다. 이 값이 0.001이라면, GRDP가 1,000원만 늘어나도 지니계수는 1이 증가한다.
당연히 상식적으로 말이 안된다. 상식적인 결과는 GRDP를 표기한 숫자가 매우 크다면 추정되는 계수의 값은 매우 작게 나올 것이라고 짐작해볼 수 있다. 예를 들어 0.00000001 정도로 작게 나와서 'GRDP가 1원 증가하면 지니계수는 0.00000001증가한다'와 같이.
이처럼 변수의 숫자가 너무 커서(= 측정 단위가 너무 작아서) 추정되는 계수의 값이 너무 작다면 보기도 안 좋을 뿐더러, 무엇보다 해석하기가 어렵다. 보통은 이런 문제를 해결하고자 적당히 단위를 조정해준다. 예를 들어 백만원 단위, 십억원 단위처럼 큰 측정단위의 GRDP로 추정한 결과를 사용하고는 한다. 그렇게 되면 GRDP 1단위는 백만원 또는 십억원일테고, 이를 표기한 숫자는 상대적으로 작아질테니 보다 해석이 쉽고 와닿는 값으로 추정될 수 있다.
단위를 조정하는 다른 방식으로 표준편차로 나눠주기도 하는데, 이 경우는 해석이 너무 까다로워진다. 그래서 로그를 취하고는 한다. 로그는 태생이 큰 값을 작게 만들어 주는 방식이므로 적합하기도 하고 측정단위를 키우는 것만으로는 해결하지 못한 부분을 해결해준다.
무슨 말이냐면, 아까 추정을 국가를 단위로 추정했다고 해보자. GRDP 대신 달러로 측정한 GDP를 사용하고 단위는 백만달러라고 해보자.
만약 그 때 추정한 결과가 0.02라면, 우리는 '다른 조건이 일정할 때 GDP가 백만달러 늘어난다면, 지니계수는 0.02만큼 상승한다.'라고 해석할 수 있다. 이 해석이 논리적으로 말은 된다.
그런데 이 결과가 모든 국가에서 일관성있고 설득력 있게 다가올까? 아마 아닐거다. GDP 한 단위인 백만달러가 미국이나 중국 같은 경제대국에 비해 아주 작은 나라에서는 매우 큰 단위이다. 평균적이라는 단서가 붙는다고 하더라도 모든 국가에서 동일한 해석을 하기에는 이번에는 측정단위가 너무 크다.
하지만 만약 'GDP가 1% 상승했을 때, 지니계수는 0.01 증가한다'와 같은 해석을 할 수 있다면 어떨까? 여전히 국가별 특성에 따라 결과를 받아 들이는 데는 차이가 있을 수는 있어도 해석은 그런대로 설득력을 갖는다.
이처럼 변수를 측정하는 단위가 매우 작아서 값이 지나치게 크게 되면 생기는 문제를 해결하면서 계수 해석의 문제까지 동시에 해결할 수 있기 때문에 로그변환을 해주고는 한다.
2) 모형(Model)의 문제
첫번째는 사실 선택의 문제이기도 하다. 앞서 밝힌 것처럼 측정단위가 너무 작다면 단위를 키워서 숫자 자체는 작게 만들어 주면 된다. 한 국가의 경제규모 등 국가별 특성에 따라 '한 단위'가 현실과 동떨어져있다고 느낀다면 다른 변수를 통제하면 일부분 해결할 수 있다. 물론 로그변환을 하는 게 훨씬 좋지만.
이에 반해 로그를 취하는 게 좋은 경우가 있다. 애초에 모형 자체가 로그를 취해야 하는 경우를 말한다. 예를 들어 중력모형이 있다. 중력 모형은 뉴턴의 중력방정식과 비슷한 형태를 띄는데, 두 물체 간의 중력을 나타내는 방정식은 아래처럼 생겼다.
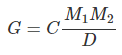
는 중력, 은 질량, 는 거리를 말한다. 말하자면 중력이라는 건 두 물체의 질량에 비례하고 거리에는 반비례한다는 의미이다. 이런 아이디어를 무역이나 외환의 교역량, 나아가 인구간의 교류(이민인구)을 설명할 때에도 사용한다. 즉 두 국가간 재화/인구 등의 교역량은 두 국가의 '경제적 질량'에 비례하고 거리에는 반비례한다는 거다. 그러니 아래와 같은 모형을 생각해볼 수 있다.
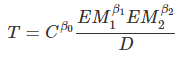
T는 교역량, EM은 경제적 질량을 말한다. 국가의 경제규모가 커질수록 교역량이 늘어나고, 국가 간의 거리가 너무 멀다면 비용문제로 교역량은 줄어들테니, 상식적으로 말은 된다.
문제는 이 모형을 바로 추정하기가 어렵다는 거다. 그래서 이 경우에는 양변에 로그를 취한다. 그러면 아래와 같은 식이 나온다.
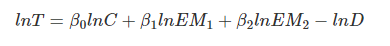
이제 적당한 선형식이 되었으니 추정하면 된다.
이런 경우와 비슷한 게 콥더글라스함수(Cobb-Douglas function)을 사용하게 되는 경우인데, 콥더글라스 생산함수는 아래와 같이 생겼다.

여기서 이면 1차동차함수인데, 각각의 값을 추정하기 위해 양변에 로그를 취해서 가설검정을 하고는 한다. 이 경우 로그를 취하지 않으면 추정이 매우, 매우 어려워 질 수 밖에 없다.
3) 데이터 생성 과정(Data Generating Process;DGP)의 문제
이 경우는 알고 있으면 아는 척 하기 참 좋다(!). 이 부분은 로그변환을 해야 하는 이론적인 근거는 될 수 있겠다. 바꿔 말하면 경제학적인 이유보다는 수학적인 이유다.
보통 확률변수의 분포가 정규분포처럼 아름다운 종모양과는 달리 로그정규분포처럼 꼬리가 긴 분포가 생기는 경우가 있다. 항상 그런 것은 아닌데, 데이터 생성과정에서 일종의 조작(?)이 생겨서 그럴 수 있다.
예를 들어서 이 세상이 매우 발달하고 공정해져서 개인의 능력에 맞게 임금을 받을 수 있다고 해보자(최저임금제는 없다고 가정한다).
그런데 누군가 아주 심각한 트롤러가 있다(!). 이 사람을 고용하면 오히려 생산이 줄어 드는 경우이다. 이렇게 되면 임금을 지불하는 게 아니라 오히려 돈을 받아야겠다(!!). 하지만 그런 일은 일어나지 않는다. 상식적으로도, 경제학적으로도 임금이 0 이하로 떨어지지는 않기 때문이다.
이처럼 어떤 변수들은 양의 실수(Real number) 내에서만 정의되는 경우가 있다. 이런 변수를 설명변수로 통제하여 추정하는 경우 원칙적으로는 곧바로 OLS로 추정을 하면 안된다. 이 변수는 양의 실수만 값으로 취할 수 있다는 제약식을 두고 추정량을 새로 구해보고, 그 값이 OLS와 같다면 그 때 OLS를 써야한다. 만약 다르다면...
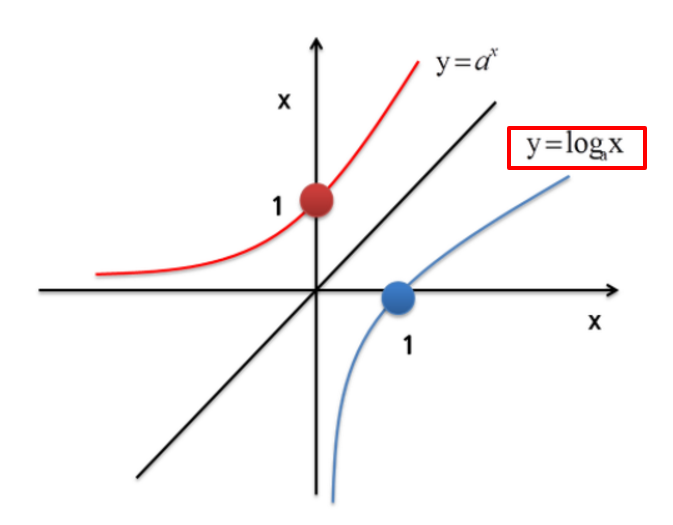
이런 문제를 피하고자 로그변환을 한다. 로그는 아래 그림처럼 정의역은 양수(Positive Real Number), 공역은 모든 실수(Real Number)이기 때문에 로그변환을 한 값은 제약식이 없는 실수이다.

로그함수(출처 : 위키백과)
따라서 로그변환을 한 변수는 그대로 OLS를 써도 무방하다. OLS추정량이 불편추정량(Unbiased Estimator)이거나 일치추정량(Consistent Estimator)인지는 별개의 문제이지만.
4) 마치며
로그변환을 하는 데에는 법칙은 없다고 했는데, 막상 3번째 이유를 보면 법칙이 있는 것 처럼 보인다. 사실 그렇다(!). 하지만 없다고 생각하는 게 낫다. 저걸 신경쓰기 시작하면 이제 변수가 음수가 아닌 이유를 DGP를 들어서 설명해야 한다. 그러지 말고, 남들이 그렇게 하는 데에는 다 이유가 있다고 생각하고 누군가 로그로 변환해서 추정했다면 그렇게 하자(!!). 그리고 만약 누군가 로그로 변환한 이유를 묻는다면 그제서야 위의 3가지 이유 중 하나를 적당히 들자(!!!).
(여담1) 간혹 '변수가 로그정규분포이기 때문에 로그변환을 해서 정규분포로 만들어준다'고 하기도 하는데, 적절한 답은 아니라고 생각한다. 변수가 로그정규분포에서 나오든, 카이제곱분포에서 나오든 가설검정 단계에서 중요한 건 추정량의 분포이지, 변수의 분포가 아니다. 로그변환을 함으로써 원래는 로그정규분포인 '추정량'을 정규분포로 만들어준다는 이야기라면 모를까, '변수'의 로그정규분포 여부는 그리 중요하지는 않다. 적어도 회귀분석을 할 때는.
3. 로그변환, 정말 옳은 방법일까?
논문 : www.ncbi.nlm.nih.gov/pmc/articles/PMC4120293/
논문 2줄 요약
1. 변환하면 결국 원본 데이터하고 값이 달라지는거다. 종종 로그변환 후 원본 데이터와 상관성이 떨어지는 경우가 있다.
2. 되도록이면 사용하지말고 다른 분석방법을 쓰자.
논문에서도 말하는 바 이지만,
원본의 데이터를 그대로 살리면서 데이터를 변환하는 것은 사실상 불가능하다.
심지어 로그를 취해 변환시켰는데, 원본 데이터의 성질을 그대로 가져오는 것은 더 힘든 일이다.(스케일링 자체가 성질변환)
하지만 전통적으로 값의 크기를 맞출 때, 계산을 편리하게 하기 위해 로그변환은 종종 사용되었고
변환을 하더라도 원본 데이터의 성질보존력이 뛰어나기 때문에 현재도 많이 사용되고 있다.
어느 정도 안정성이 확보된 스킬이기 때문에 아무 생각없이 사용하는 것이 아니라면 무방하다고 판단한다.
'데이터분석&캐글' 카테고리의 다른 글
| 사람들이 선형회귀에 대해 잘못 알고있는 점 (0) | 2021.02.19 |
|---|---|
| 데이터 시각화 함수 정리 _Seaborn (0) | 2021.01.21 |
| 캐글코리아 커널 커리큘럼 (0) | 2021.01.20 |
| Kaggle로 알아보는 데이터 분석사고 (0) | 2021.01.20 |
| 범주형 자료 Encoding for Handling (0) | 2021.01.16 |


